ალუმინის შენადნობის წონის გაანგარიშების ფორმულის ცხრილი

1. ძირითადი ფორმულის ფიზიკური პრინციპის შემოწმება

მასის შენახვის კანონი

ყველა ფორმულა ეფუძნება m=ρ×V-ის ფიზიკურ ბუნებას (მასა = სიმკვრივე × მოცულობა).

სიმკვრივის მნიშვნელობა

სუფთა ალუმინის თეორიული სიმკვრივე: 2,698 კგ/მ³ (20℃)

სამრეწველო გამოთვლებისთვის (შეცდომა < 0.1%) სავარაუდო მნიშვნელობა 2,700 კგ/მ³-ია.

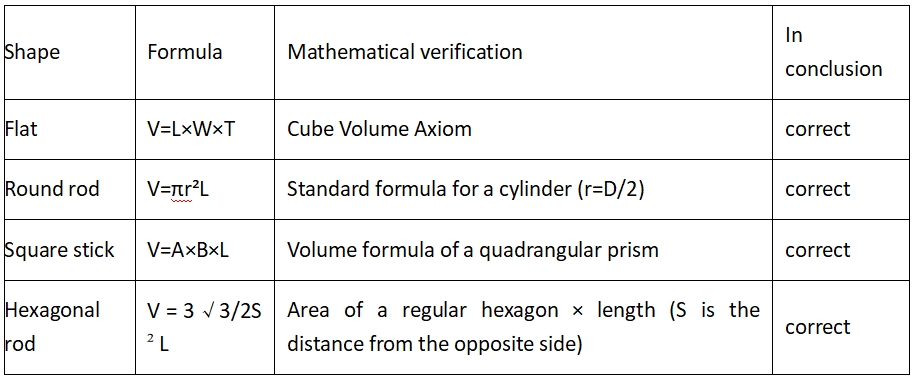
2. გეომეტრიული ფორმულების სიზუსტის დადასტურება

2.1. სტანდარტული გეომეტრიული მოცულობის ფორმულა

2.2. მილის ფორმულის სიღრმისეული შემოწმება

კვადრატული მილის ფორმულის შეზღუდვები:

ეს მაშინ ხდება, როდესაც მილის კედლის სისქე ერთგვაროვანია და შიდა კუთხე მართია (ნამდვილ კვადრატულ მილს მომრგვალებული გადასასვლელი აქვს და თეორიული შეცდომა დაახლოებით 1-3%-ია).

3. ერთეულის სისტემის თანმიმდევრულობის შემოწმება

ერთეულებს შორის გაანგარიშების რისკის წერტილის კვლევა

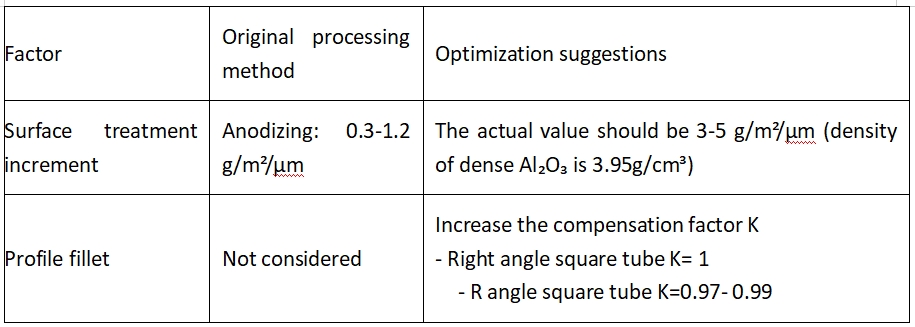
4. საინჟინრო შესაფერისობის შესწორება

4.1. არაიდეალური ფაქტორების კომპენსაცია

4.2. ტოლერანტობის ზემოქმედების რაოდენობრივი განსაზღვრა

სისქის ტოლერანტობა ±10% → წონის გადახრა ±(8% ~ 12%) (თხელკედლიანი ნაწილები უფრო მგრძნობიარეა)

ამოხსნა: W ფაქტობრივი = W თეორიული × (1 + Δt / t) (Δt : სისქის გადახრა)

5. სასაზღვრო მდგომარეობის ტესტი

ექსტრემალური შემთხვევის დადასტურება:

სიმკვრივის ანომალიის სცენარი

7xxx შენადნობი (7075): გაზომილი სიმკვრივე 2.810 გ/სმ³ → თუ შეცდომით გამოიყენება 2.7 გ/სმ³, შეცდომა +4.1%-ია.

ფორმულის ცხრილი

4t(A + B)- 4t² არის სტანდარტული საინჟინრო გაანგარიშება, რომელიც გამოითვლება მონაკვეთის პერიმეტრის კედლის სისქეზე გამრავლებით და შემდეგ ოთხი კუთხის გამოკლებით.

გაანგარიშების მაგალითი:

1.6061 ალუმინის ფირფიტა(1000 × 500 × 10 მმ, სიგრძე 2 მ): სიგანე = 1000 × 500 × 2 × 0.0027 = 27 კგ

2.7075 მრგვალი მილი(გარე დიამეტრი 50 მმ, კედლის სისქე 3 მმ, სიგრძე 1.5 მ): W = [(50-3)×3×3.1416×1.5]×0.00283 ≈ 5.65 კგ

3. კვადრატული მილი(40×40×2 მმ, სიგრძე 3 მ): W = [2×2×(40+40-4)×3]×0.0027×0.98 ≈ 2.42 კგ

რეკომენდებული სამუშაო პროცესი

1. სიმკვრივის შერჩევა → 2. ფაქტობრივი ზომის გაზომვა → 3. კომპენსაციის კოეფიციენტის შერჩევა → 4. ფორმულით გამოთვლა